Solving the peg game with TLA+

Introduction

In this post, I’ll use TLA+, which is a formal specification language based on temporal logic, to solve an old favorite of mine: the “Cracker Barrel peg game”.

The Peg Game

This game is also formally known as triangular peg solitaire. And, according to Wikipedia, the game mechanics work as follows:

The standard game fills the entire board with pegs except for the central hole. The objective is, making valid moves, to empty the entire board except for a solitary peg in the central hole. A valid move is to jump a peg orthogonally over an adjacent peg into a hole two positions away and then to remove the jumped peg.

So, where does TLA+ come in?

The TLA+ specification

In order to solve a problem with TLA+, what we really do is specify the rules of the system—a TLA+ “program” is called a specification. So, we’ll be specifying the rules of the peg game, and with TLA+ we do this using set theory and temporal logic.

Once we model/specify the game, we can ask TLA+ any question about the game we want, and it will answer it for us. For example: “how many possible unique peg-game possibilities are there?”, or “is it possible to, after 12 moves, end a game with only the pegs (1,1) and (1,5) remaining?”. The question we’ll be asking is “what steps should we take to win?.

Before we design our specification, let’s clarify some TLA+ fundamentals.

There are excellent TLA+ tutorials online but I’ll recap, really quick, the minimum you need to know to understand the specification I’ve provided.

TLA+ is based on temporal logic. To put it briefly, this means you are modelling the system as a cyclic graph of states using set theory, where each state is simply a mapping of variables to values, and states transition between each other according to mathematical functions based heavily on set theory.

For a minimal TLA+ specification, you should expect to define one or more variables, one or more functions, a special Init function, and a special Next function.

For example, in the diagram shown above, each node represents a state, and the edges represent transitions between states. To be exact, it could be described as follows:

VARIABLES x
Init == x=1
Next == (x'=x+5 ∨ x'=x*3)

To elaborate:

• Variables: These have a single value at any given step, but may change from one step to the next (in accordance with the Init and Next functions). They’re defined in a single header, e.g., VARIABLES x, y, z, etc.
• Functions: These naturally close over all variables, can optionally take one or more arguments, and return a single value. (Defined using ==, e.g., f == x+y+z or g(n) == x+n.)
• Init: This is a special function (which happens to be a predicate—a boolean function) which defines what the initial state(s) of the system are. Any set of (variable→value) mappings which causes this function to return True will be included as an initial state. For example, Init == x=1 means the initial state(s) are any state(s) where x equals 1—in this case there is only one state (x=1) for which this resolves to True, so there is only one initial state. (In contrast, if we would have used Init == x*x=4, there would be two initial states: x=-2 and x=2.)
• Next: This is a special function/predicate which, given any state, defines what the next state(s) of the system are. The ' suffix should be read as “next state of”. For example, Next == x'=x+1 means the next state(s) are those where the next value of x is the previous value of x plus 1. In the example given above, Next == (x'=x+5 ∨ x'=x*3) means the next state(s) are those where the next value of x is the previous value of x plus 5, or, where the next value of x is the previous value of x times 3. (Note how there can be a varying number of Init and Next states!)

Now that we’ve clarified some TLA+ fundamentals, let’s get back to coding specifying the peg game!

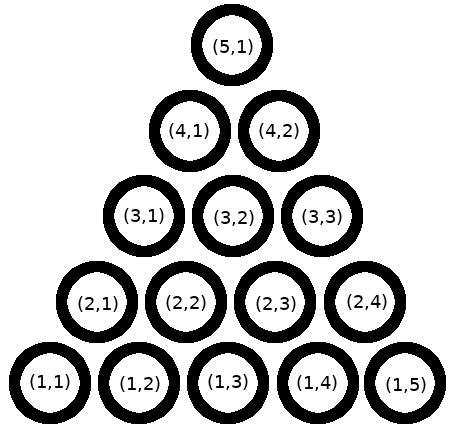
Again, we need to model the peg game according to the rules we described earlier. First, we’ll refer to each hole as a “spot”, and give each spot a number (well, an ordered pair of numbers). This means we have this list of all possible “Spots”. We’ll need to tell TLA+ that.

We can define a function named Spots, which returns the entire list of spots, like so:

Spots == { <<x,y>> \in {1,2,3,4,5}\X{1,2,3,4,5} : x+y<=6 }

…or, alternatively…

Spots == { <<x,y>> ∈ {1,2,3,4,5}⨯{1,2,3,4,5} : x+y<=6 }

This can be read as “Spots equals the set of all (x,y) combinations where x∈{1,2,3,4,5}, y∈{1,2,3,4,5}, and x+y<=6”. This is just a shorter way of writing Spots == [(1,1),(1,2),(1,3),(1,4),(1,5),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(4,1),(4,2),(5,1)].

Spots doesn’t change from turn to turn. Though we’ve defined it as a function, you can think of it as constant. But not all of our values are constant: in any turn-based game, there is always the concept of a current state, which changes after each turn. And in our game, the current state is fairly simple: it can be summarized by the subset of Spots which have currently have pegs. Since this state will change from turn to turn, we’ll put it in a TLA+ variable. We can simply create a single variable, called state:

VARIABLES state

(Please be aware that, in general, “the state” refers collectively to the current values of all variables. But, in this case, we only have one single variable, so we’ve simply named it state, but we could have named it, for example, activepegs.)

According to the official peg game rules, the initial state of the board will be when all Spots are filled except for (3,2).

We can declare that with the following:

Init == (state = Spots \ { <<3,2>> })

(Note that A \ B denotes logical relative complement, i.e., “all elements in the set A but not B”.)

As I explained earlier, Init is a special function in TLA+, and is called the initial state function (or initial state predicate). It may be confusing that I’m setting Init “equal” the result of another equation, so I’ll offer a different perspective: with this line, don’t think of it as “defining” or “assigning” the Init condition to this expression, think of it as constraining the initial possible values of all of our variables. In our case, we happen have a single variable, and we happen to be locking it down to one single value.

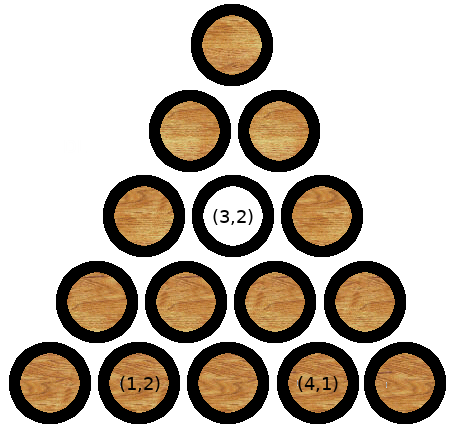
Now that we’ve defined the initial state of the game, we’ll need to talk about how to move pegs around. For example, during our first move from the starting state, we only have two ways to get to the next state:

1. Move (1,2) up-right to (3,2), or
2. Move (4,1) up-left to (3,2)

I already explained how “next states” work, but I’ll say it again: in TLA+, we model state changes by specifying the mathematical relationship between the current state of our variables (in this case, just state) and the next state of our variables (state'). Remember that TLA+ will recognize the ' suffix of state' to mean “the next value of state”.

Formally, we can specify what constitutes a valid next state with the Next condition:

Next == ∃ <<x,y>> ∈ Spots : 
             (CanJumpUpRight(x,y)   ∧ state' = JumpUpRight(x,y))
           ∨ (CanJumpDownLeft(x,y)  ∧ state' = JumpDownLeft(x,y))
           ∨ (CanJumpUpLeft(x,y)    ∧ state' = JumpUpLeft(x,y))
           ∨ (CanJumpDownRight(x,y) ∧ state' = JumpDownRight(x,y))
           ∨ (CanJumpRight(x,y)     ∧ state' = JumpRight(x,y))
           ∨ (CanJumpLeft(x,y)      ∧ state' = JumpLeft(x,y))

This probably looks intimidating. A quick guide to the symbols:

• <<x,y>> means “the ordered pair (x,y)”
• ∃ e ∈ s : p means “there exists an element e from the set s where p is true”
• ∧ means “and”
• ∨ means “or”

Also, I’ve snuck in several (related) functions (not defined yet) which really boil down to following two, except all in different directions:

• CanJumpUpRight(x,y) will true if, in the board’s current state, there is a peg at position (x,y), and it’s allowed to jump up-right according to the peg game rules.
• JumpUpRight(x,y) will return the set of pegs which will be left on the board if we do choose to jump up-right from the current state. (Note that it doesn’t actually do anything, because it’s just a function!)

And if we fully translate the above definition of Next to english, it reads:

A next state (state') is a valid next move from the current state if and only if there exists some (x,y) spot in the current state which CAN jump in some direction (UpRight, DownLeft, etc.) , and also, the next state is the result of jumping in that direction.

Here are the complete definitions of each “CanJump” and “Jump” function:

CanJumpUpRight(x,y) == (<<x,y>> ∈ state
                       ∧ <<x+1,y>> ∈ state
                       ∧ <<x+2,y>> ∈ (Spots \ state))
                    
CanJumpDownLeft(x,y) == (<<x,y>> ∈ state
                        ∧ <<x-1,y>> ∈ state
                        ∧ <<x-2,y>> ∈ (Spots \ state))

CanJumpUpLeft(x,y) == (<<x,y>> ∈ state
                      ∧ <<x+1,y-1>> ∈ state
                      ∧ <<x+2,y-2>> ∈ (Spots \ state))
                    
CanJumpDownRight(x,y) == (<<x,y>> ∈ state
                         ∧ <<x-1,y+1>> ∈ state
                         ∧ <<x-2,y+2>> ∈ (Spots \ state))

CanJumpRight(x,y) == (<<x,y>> ∈ state
                     ∧ <<x,y+1>> ∈ state
                     ∧ <<x,y+2>> ∈ (Spots \ state))
                       
CanJumpLeft(x,y) == (<<x,y>> ∈ state
                    ∧ <<x,y-1>> ∈ state
                    ∧ <<x,y-2>> ∈ (Spots \ state))

JumpUpRight(x,y)  == (((state \ {<<x,y>>}) \ {<<x+1,y>>}) ∪ {<<x+2,y>>})   

JumpDownLeft(x,y) == (((state \ {<<x,y>>}) \ {<<x-1,y>>}) ∪ {<<x-2,y>>})

JumpUpLeft(x,y)    == (((state \ {<<x,y>>}) \ {<<x+1,y-1>>}) ∪ {<<x+2,y-2>>})

JumpDownRight(x,y) == (((state \ {<<x,y>>}) \ {<<x-1,y+1>>}) ∪ {<<x-2,y+2>>})  

JumpRight(x,y) == (((state \ {<<x,y>>}) \ {<<x,y+1>>}) ∪ {<<x,y+2>>})   

JumpLeft(x,y)  == (((state \ {<<x,y>>}) \ {<<x,y-1>>}) ∪ {<<x,y-2>>})

The game is now mostly specified, but we yet defined yet what it means to “win”. We’ll want to define a function that returns true if the current state is in a winning position. For this game, it’s pretty simple: if there’s only one peg left, we’ve won:

Win == Cardinality(state) = 1

(The Cardinality function is a built-in TLA+ function which counts how many elements are in a set.)

To “ask” TLA+ to find a winning state, we can use the TLA+ toolbox’s “model checker”:

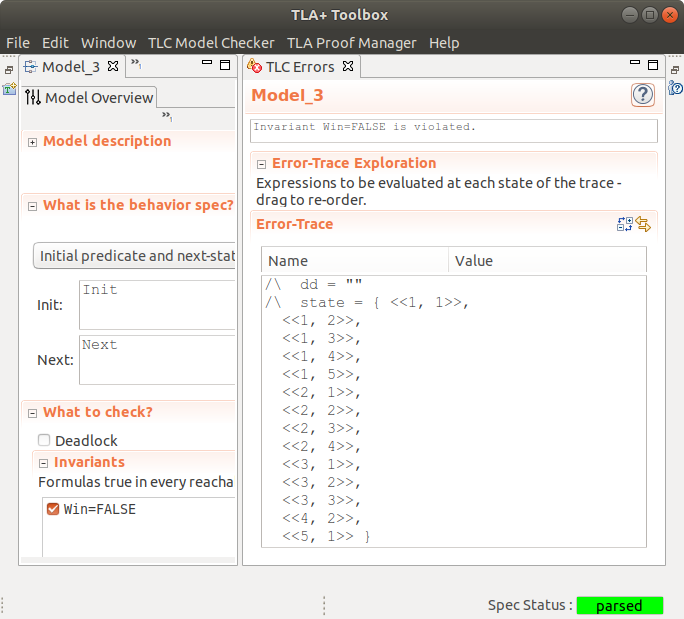
What I’ve done here is asked TLA+, “Please verify that there are no winning states; i.e., for all states, Win is always False.” It found that this is false, and gave evidence.

The complete source code can be found on GitHub.

(Note that, if you read the source code, you’ll notice that I’ve added additional variables: xx, yy, and dd. This is essentially a hack to get TLA+ to print out the entire history of states, rather than just the final, winning state. There are probably better ways to do this, but this works!)